¡SkyCaramba! Weekly astronomy blog for the week ending July 11, 2015
Some objects orbit other objects in nearly perfect circles. Others orbit in distinct ovals or ellipses. And others turn near another object, veer away, and never return. There’s a way to mathematically represent these variations. It’s called eccentricity.
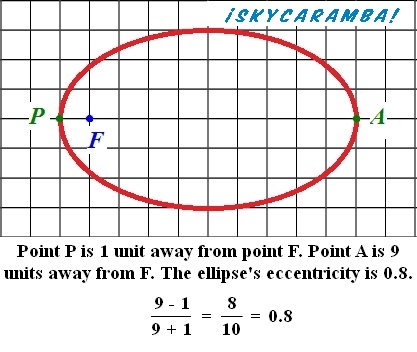An orbit that’s a perfect circle has no eccentricity at all. So, its eccentricity is said to be 0. Many satellites orbiting Earth are required to be in the same place in the sky at all times. They are put in orbits with eccentricities of 0.
If the orbit is just a little elliptical, its eccentricity must be a little more than 0. Venus has an eccentricity of 0.0068. It’s 109 million kilometers from the sun at aphelion and 107 million kilometers away at perihelion. It’s the most circular of the planets’ orbits in our solar system.
Earth’s orbital eccentricity is 0.0167. At aphelion in early July, our planet is 152.1 million kilometers from the sun. At perihelion in early January, the distance has shrunk to 147 million kilometers.
Mercury’s orbit is much more elliptical with an eccentricity 0.2056. The planet’s distance from the sun ranges from 69.9 million kilometers at most to 46.1 million kilometers at the least.
Comets tend to have much higher eccentricities, so their farthest distances from the sun is many times more than their closest. Comet Halley’s comes in at 0.967. Hyakutake, one of the great comets of the 1990s, has an eccentricity of 0.9998. If the eccentricity is just a little higher, at exactly 1, the orbit is parabolic. According to some definitions, that’s not an orbit at all because the object will leave and never return.
Some comets have ecc
entricities higher than 1, but not much. The highest belonged to a comet discovered in 1980. It was 1.057. Such an orbit is called hyperbolic. Like a parabolic orbit, a hyperbolic orbit is one of no return. The hyperbolic orbit’s tracks are closer to straight lines on approach and departure.
For an elliptical orbit, there are two ways to calculate eccentricity. The easiest is to take the farthest distance in orbit and subtract the closest. Divide that figure by the sum of the farthest and closest. So for Earth (measuring distances in millions of kilometers):
(152.1 – 147.1) ÷ (152.1 + 147.1) = 5 ÷ 299.2 = 0.0167
However, this formula doesn’t work for hyperbolic orbits, because the farthest point is infinity. It’s a little more complicated, but there is a formula that works for all orbits that aren’t circles. It requires the person calculating it to determine where to place a line called the directrix. Then the object’s distance from what it’s orbiting is divided by its distance from the directrix. Since the article is nearing full length and we’re getting into mathematics that some people aren’t fond of, I’ll end here. I encourage anyone so inclined to look into the formula on his or her own.
¡SkyCaramba!